

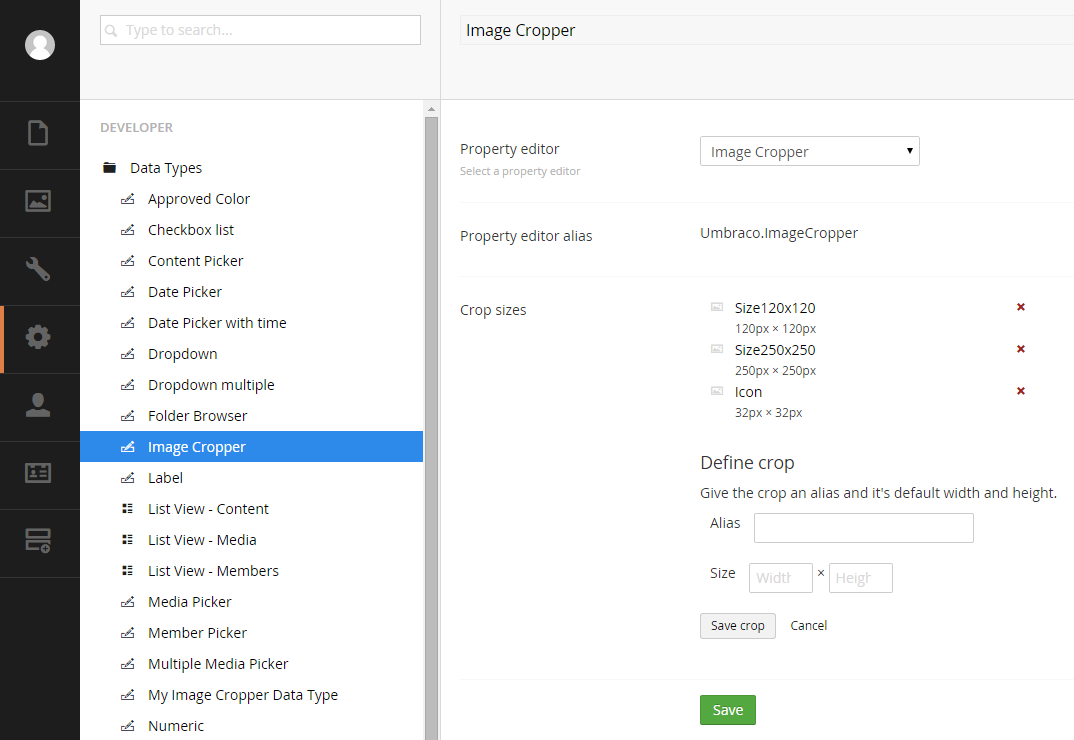
Image Cropper allows the administrator to upload an image for which the Umbraco will create copies of the image with dimensions that we define. The first thing that we have to do is to define the dimensions of the images that we want Umbraco to create for us. To do this we click with the mouse on the node Data Types of Developers section and select the data type Image Cropper to display the administration screen of the data type.
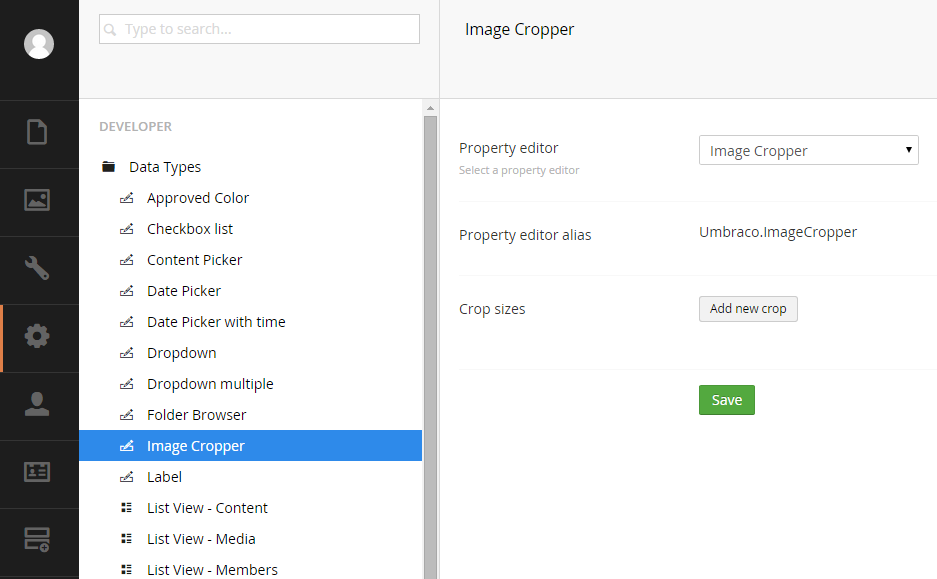
In order to create a new dimension we press the button Add new crop and the new dimension form will appear on the screen.
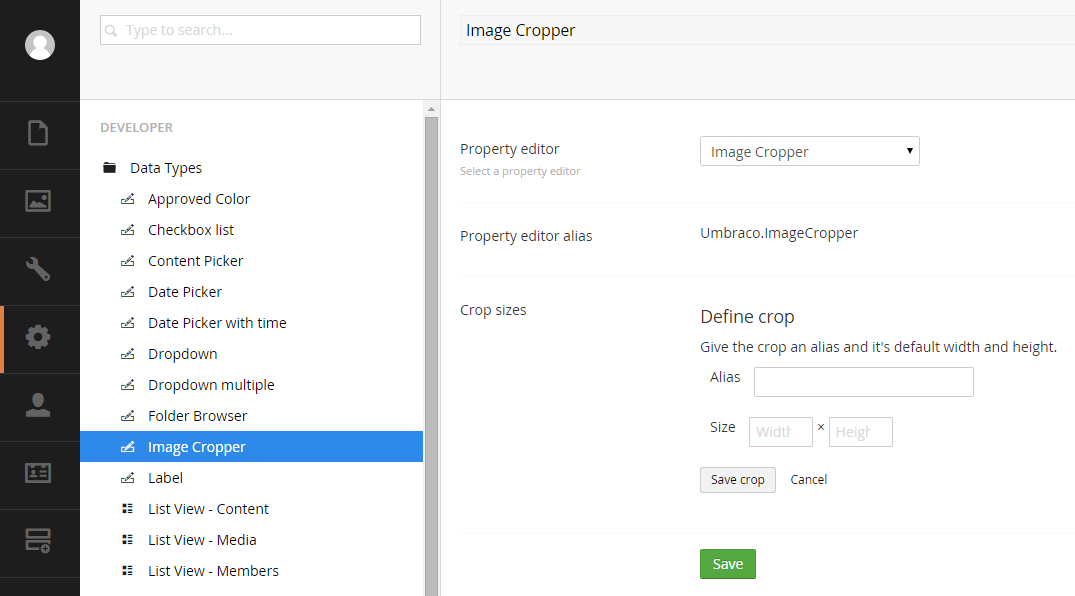
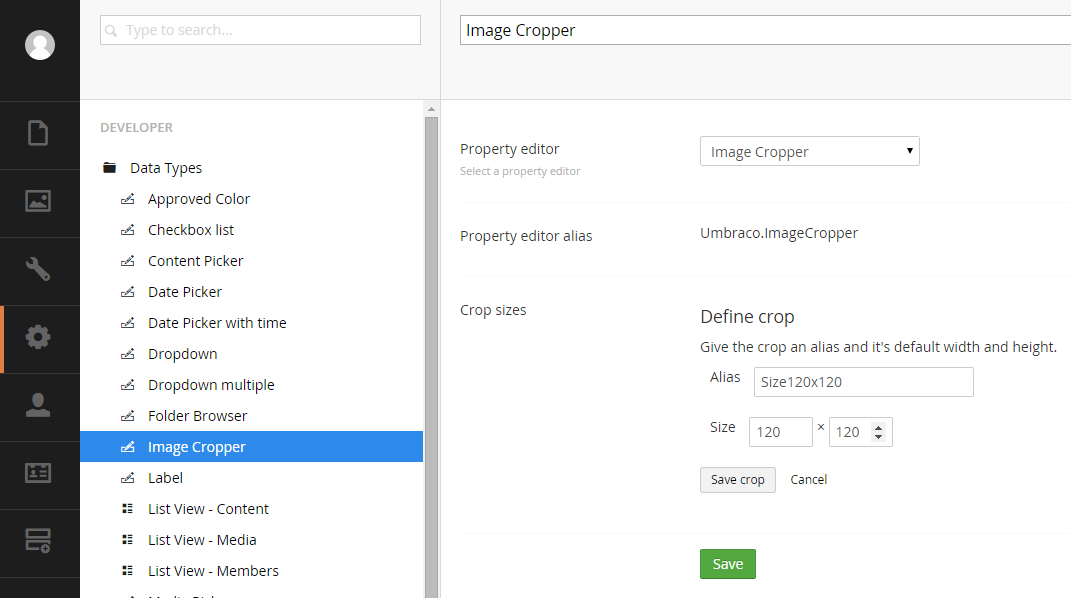
In the Alias text box we type the alias of the new dimension and the in the Width and Height text boxes we type the width and height that we want for the image. In order to save the new dimension we have to press the button Save crop.
After saving the image size, it appears as an option on the screen where there is a red x to click in case that we want to delete it.
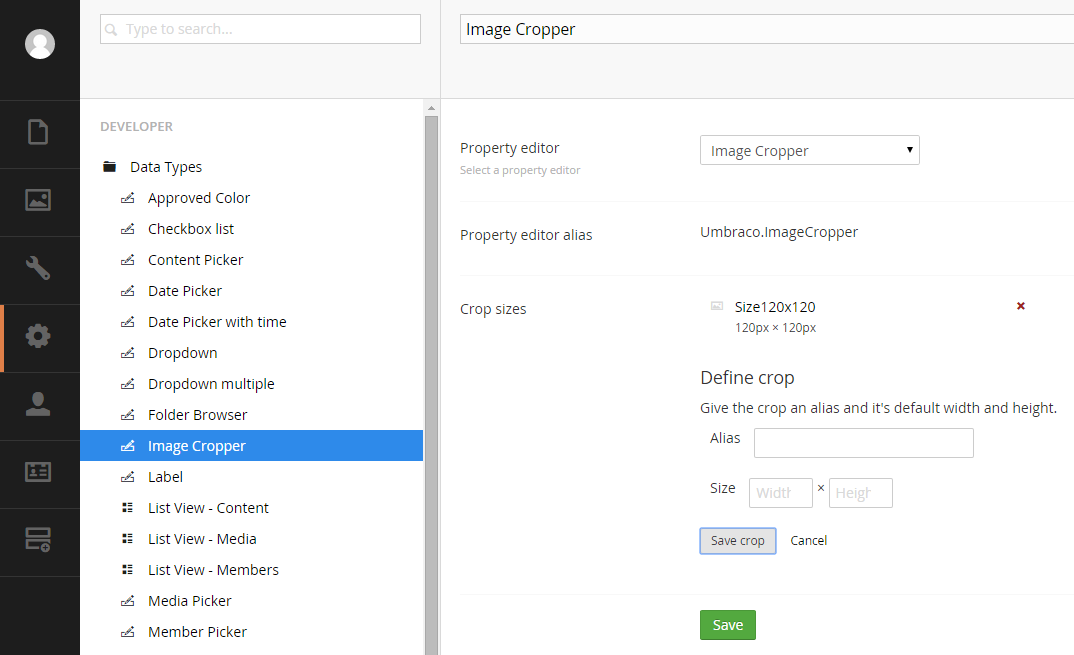
Using the same approach we can add more image sizes.
Now that we have added the sizes we want to make properties of type Image Cropper in Document Types in Umbraco. Below we can see an example of creating a property of type Image Cropper:
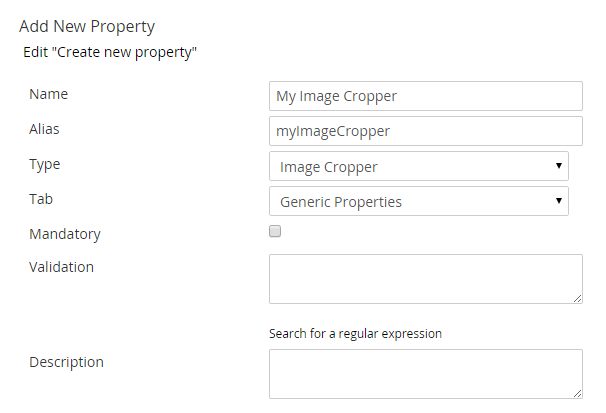
The My Image Cropper property has the following appearance when we edit the document:
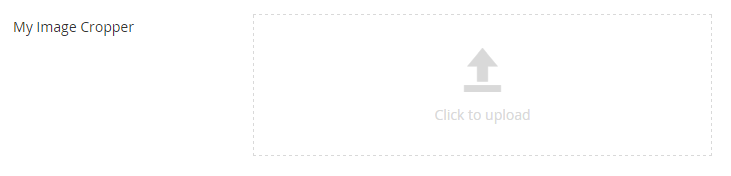
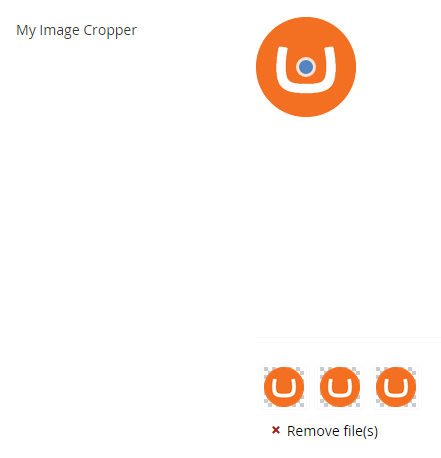
To choose the image for which the Umbraco will automatically create the resized images we defined, we should click on the icon with the up arrow. On our screen will appear the Open dialog box to select the image we want. After selecting the image we press the Open button to complete the process.

In our property the image appears on which there is a dot. This dot can be moved with the mouse to define where we want to be the center of the image after resizing. This point does not have to be the center of the image. Umbraco will resize the image and try to bring this point as close as possible to the center of the final image. Under the picture with the dot we can see how the three different versions of sizes that we have defined will appear on the screen. On the screen we can find a red x with the label Remove file (s) so that we will be able to delete the image if we want to replace it with another picture.
To get the URL of the image with property name myImageCropper and alias name Size120x120 as a strongly typed object we use the following code:
@if (CurrentPage.HasValue("myImageCropper"))
{
<img src='@CurrentPage.GetCropUrl("myImageCropper", "Size120x120")' />
}In order to read the value using dynamic properties we use the following code:
@if (CurrentPage.HasValue("myImageCropper"))
{
<img src='@Model.Content.GetCropUrl("myImageCropper", "Size120x120")' />
}The GetCropUrl method allows us to define the size we want to have the image. In order to do it we can use the following syntax:
@if (CurrentPage.HasValue("myImageCropper"))
{
<img src='@Model.Content.GetCropUrl(propertyAlias: "myImageCropper", height: 100, width: 200)' />
}From Umbraco version 7.1 ImageProcessor has been added which allows us to apply different effects to the displayed image. Below we can see an example of using the ImageProcessor:
@if (CurrentPage.HasValue("myImageCropper"))
{
<img src='@CurrentPage.GetCropUrl("myImageCropper", "Size120x120")&blur=3,sigma-1.5,threshold-10' />
}More information about ImageProcessor can be found in the project page which is http://imageprocessor.org/.